Before I begin, I want to emphasize that all commands can be found in the IBM ILOG CPLEX documentation. My intent is to summarize commonly used CPLEX Python commands for performing a modeling task and solving mathematical models. For me, this cheat sheet of CPLEX Python API commands has always been a great help. Also, it is very difficult to accommodate all the commands as they are many. I am updating the CPLEX Python API commands here according to my usage. Therefore, next time you visit this page, you may find more commands than now.
For an easy explanation, I will use the following small linear programming problem.
(LP) 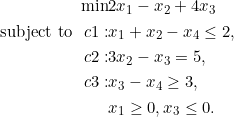
1. Create a model with no input data
model = cplex.Cplex()Our first target is to use CPLEX for writing the model ![]() . So, we start with an empty model.
. So, we start with an empty model.
2. Add Variables information to the model
model.variables.add(obj = variables_objective_coefficients,
ub = variables_upper_bounds,
lb = variables_lower_bounds,
names = variables_names)
The following (input) parameters are available to us for the modeling:
1. Variable names = ![]()
We just write them without the subscripts and add them to a list.
variables_names =[x1, x2, x3, x4].
Note: If you want to add only the variable name and the information about the coefficients and limits separately, just use the following command:
model.variables.add(names = variables_names)
2. We have objective coefficients, i.e., the coefficients assigned to the variables of the objective function: 2 x1+ (-1) x2 + 4 x3 + 0 x4. Let’s add them to a list.
variables_objective_coefficients = [2, -1, 4, 0]
model.variables.add(obj = variables_objective_coefficients, names = variables_names)
3. The Lower and the upper bounds information associated to each variables.
The bounds are the trivial constraints in the model. Cplex sets zero (0) as the lower bound for all variables by default, unless we specify it. Similarly, the upper bounds are set to very high values (example: cplex.infinity).
Also read – Column Generation for Cutting Stock Problem – LetsGyan
3. Update Objective function, and bounds information of variables in the model
1. Getting the existing objective coefficient values (in a list “objective_value_list”) from the model
objective_value_list = model.objective.get_linear()Note: If we want to get the objective coefficient of a particular variable, we can pass the variable name or its index to the get_linear() function as follows -.
coef_of_x1 = model.objective.get_linear("x1") or
coef_of_x1 = model.objective.get_linear(0)
2. To update the objective coefficients, we need to pass the (index of a variable, value) or the (var_name, corresponding_coefficient) pair. For example, if we want to set zero coefficient to the above model, we require the following command-
model.objective.set_linear([(0,0.),(1,0.), (x3,0),(x4,0.)])Now, to update the objective function in the model (again as mentioned in the LP1 example) with objective coefficient [2, -1, 4, 0]
model.objective.set_linear([(0,2),(1,-1), (x3,4),(x4,0)])3. To get the upper and the bound bounds information of a variable – for example x2.
Pass “x2” as an input argument –
ub_x2 = model.variables.get_upper_bounds("x2") or pass index of the variable –
ub_x2 = model.variables.get_upper_bounds(1)If one wants to fetch upper bounds of all the variables. Just hit the command without any argument
ub = model.variables.get_upper_bounds()Similarly, we can do for finding the lower bound from the model.
4. To update the bound information. We pass the (id, value) or the (name, value) pair. For our example, let us update the upper bound of x3 as 0.
model.variables.set_upper_bounds(x3, 0) or model.variables.set_upper_bounds(2, 0)4. Add constraints information to the model
To include the parameters and variables of the constraints in the model, we must first create a list of list pairs, one for indices (or variable names) and one for the corresponding coefficients. Each entry in the list of list pairs corresponds to a constraint. For our example, list of list pairs,
ind_list = [0,1,3], [x2, x3], [2, 3]
val_list = [[1.0,1.0,-1.0], [3.0, -1.0],[1, -1.0]]
linear_constraints_rows = [cplex.SparsePair(ind = ind_list[i], val = val_list[i]) for i in range(len(ind_list))]
linear_constraints_rows consists of three entries, each corresponding to a linear constraint. Also, the constraints name list, a list consists of the type of inequalities to each constraint and the list consists of the rhs values are:
linear_constraints_names = [“c1”, “c2”, “c3”]; linear_constraints_senses = [“L”,”E”,”G”]; Here “L”, “E” and “G” represent less than and equals (![]() ) , equal(
) , equal(![]() ), and greater than and equal (
), and greater than and equal (![]() ) signs, linear_constraints_right_hand_sides = [2,5,3].
) signs, linear_constraints_right_hand_sides = [2,5,3].
model.linear_constraints.add(lin_expr = cplex.SparsePair(linear_constraints_rows),
senses = linear_constraints_senses,
rhs = linear_constraints_right_hand_sides,
names = linear_constraints_names)
Here also, we can add the information of senses, rhs, names and linear_constraints separately.
5. To set type of the Problem – Minimization or Maximization
In our case, its a minimization problem. We can set it as follows:
model.objective.set_sense(model.objective.sense.minimize)If we want to know the type of the problem, we use the following command to find the sense of objective function –
model.objective.sense[model.objective.get_sense()]6. Solving the Cplex model
We have created our LP1 cplex model instance. Now we will solve it. Before solving it, we need to input the linear programming method for solving the model.
1. primal, dual and barrier are the three popular and widely used methods to solve general linear programming model.
alg = model.parameters.lpmethod.values
model.parameters.lpmethod.set(alg.primal) # Primal
model.parameters.lpmethod.set(alg.dual) # Dual
model.parameters.lpmethod.set(alg.barrier) # Dual
2. Once, we set the linear programming method, we can simply a solve function –
model.solve()7. Fetch Objective value, optimal solution, dual value, reduced costs information from the model after the solve
1. Optimal objective value – the model returns a single valued output as the optimal objective value from the following command –
obj_value = model.solution.get_objective_value()2. The optimal solution is the list returned by the following command –
sol_list = model.solution.get_values() #return The value sol_list[i] is the value of a variable with index ‘i’ in the solution of the model.
3. Similarly, the reduced costs and dual will be the lists of sizes equal to the number of constraints and variables respectively. We fetch them from the solution using the following commands –
dual_list = model.solution.get_dual_values()
red_list = model.solution.get_reduced_costs()4. Note that, if we want to fetch solution or paramteric information of some variables or constraints, just pass the list of indices of those variables or constraints.
For example, to fetch the dual value associated to the constraints c2 and c3 having indices 1 and 2, we do the following –
some_dual_list = model.solution.get_dual_values([1,2]) or
some_dual_list = model.solution.get_dual_values(["c2","c3"])
Similarly, getting the reduced costs and solution value of x1 we use the following commands –
x1_sol_value = red_list = model.solution.get_values('x1') or pass the index
x1_sol_value = red_list = model.solution.get_values(0)
for reduced cost -
x1_sol_value = red_list = model.solution.get_reduced_costs('x1') or pass the index
x1_sol_value = red_list = model.solution.get_reduced_costs(0)
8. Update values in the interaction matrix and RHS vector
8.1 Update rhs: For example, update rhs of constraint c2 by 2.
model.linear_constraints.set_rhs("c2", 2.0)
8.2 Update constraint name, change the name of constraint c2 to “const2”
model.linear_constraints.set_names("c2", "cons2")
8.3 Update the sense, change the sense “=” to “>=” in constraint c1.
model.linear_constraints.set_senses("c1", "G")
8.4 Update the entry in interaction matrix (A). For example, updating coefficient of x1 in “c1”.
model.linear_constraints.set_linear_components("c1", [["x1"], [2.0]])
8.5 The other command for the same –
model.linear_constraints.set_coefficients("c1", "x1", 2.0)
9. Fetch values from the interaction matrix and RHS vector
9.1 Get number of constraints in the model
model.linear_constraints.get_num()
9.2
10. Delete row and columns from the model.
10.1 Delete from by index or name of the constraint, or you can also pass a list of names or indices of constraints.
model.linear_constraints.delete(0) or
model.linear_constraints.delete("C1")10.2 Likewise, we can do for variables.
model.variables.delete(0) or
model.variables.delete("x1")