Column Generation for Cutting Stock Problem

Cutting Stock Problem: A tutorial with example to understand Column generation

Column generation is an efficient technique to solve large-sized mathematical programs. It is also called delayed-column generation due to its nature to solve the problem. It is firstly studied and applied for the Cutting stock Problems, recognized by a Soviet mathematician and economist Leonid Kantorovich in 1939.

Cutting Stock problem example

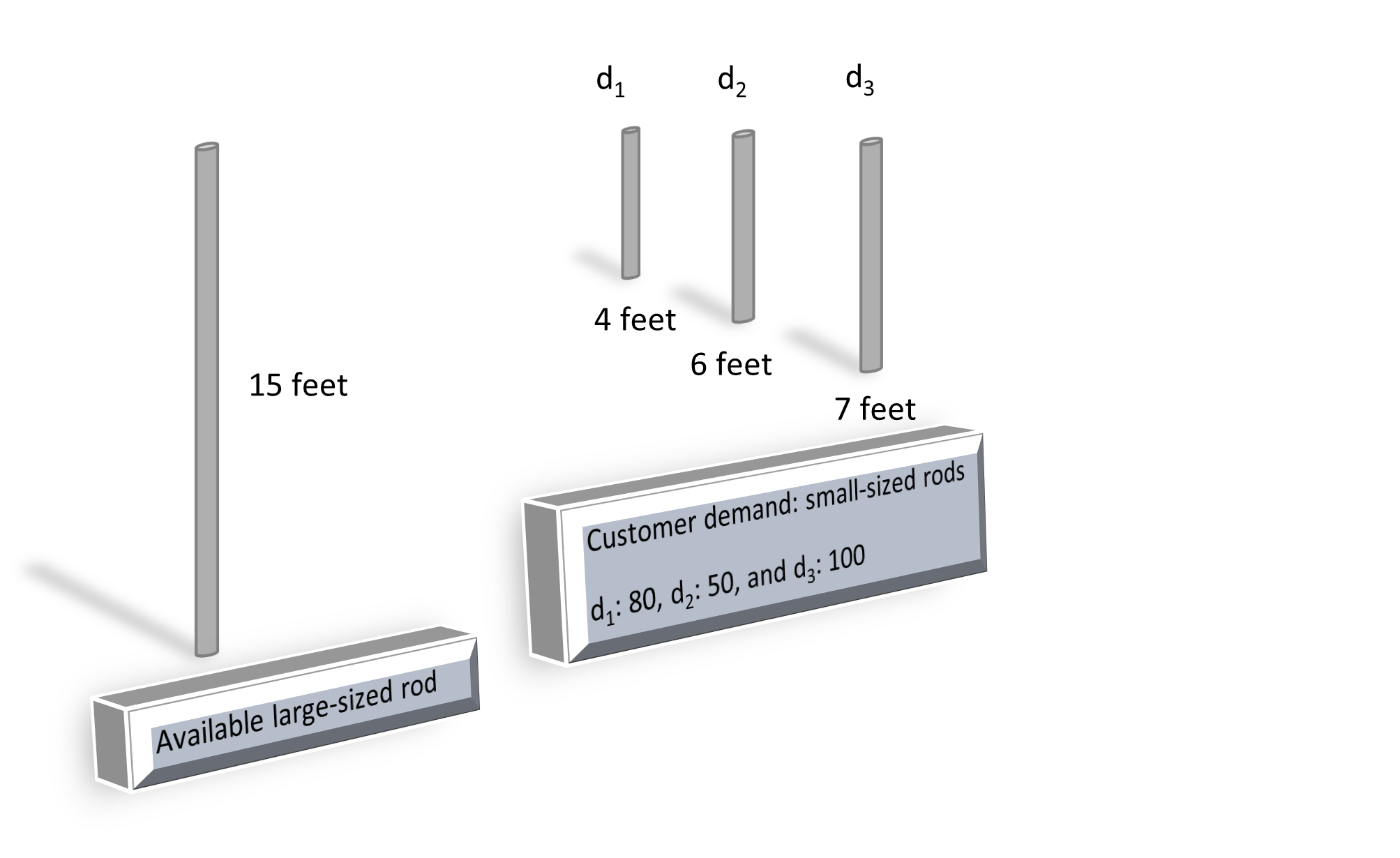
A Cutting stock problem is the problem of cutting off a minimum number of large-sized items to fulfill the customer requirements of various small-sized items of different quantities. For example, in the steel manufacturing industry, we have a stock of large-sized rods, each with a size of feet. The customer requires three different types of rods, 1) rods, each with the size of 4 feet, 2) rods of size feet, and 3) rods, each with the size of feet. Let us call them demand order types , , and . The objective is to meet the customer’s demand by cutting a minimum number of possible large-sized rods. We study Column Generation for Cutting Stock which is generally studied in most of the literature.

The cutting stock problems are interesting – for the customer’s requirement with different items, problems become difficult. Suppose a customer asks for different rods. There will be various ways to cut the large-size rod to fulfill the customer’s demand. From the above example, the possibilities of producing required rods from a large-sized rod are

1. cuts of ; waste =
2. cuts of ; waste =
3. cuts of ; waste =
4. cuts of and cut of ; waste =
5. cut of and cut of ; waste =
   
   
   And many such combinations of possibilities to meet the total demand.

Idea -1: A dummy heuristic for Cutting Stock Problem

To solve this problem, the first (dummy) idea that comes to mind is to pick the large-sized rod and start cutting it until we produce the desired demand orders. The demand requirement is fulfilled one by one, i.e., first, we meet the demand type, then , and then .

Let us do a simple python implementation for this –

large_size_rod_used = 0 
demand_size = [4, 6, 7]
demand_count = [80, 50, 100]
large_len = 15 
effective_len = large_len
waste = 0

for i in range(3):
    while (True):
        if (demand_count[i] > 0) :
            if (demand_size[i] <= effective_len):
                effective_len = effective_len - demand_size[i]
                demand_count[i] = demand_count[i] - 1
            
            else:
                large_size_rod_used = large_size_rod_used + 1
                waste = waste + effective_len
                effective_len = large_len
                continue
        else:
            break
print("large_size_rod_used ", large_size_rod_used)
print("total waste ", waste)

Let us run this:
We see that, to meet the demand, the total number of large-sized rods used is = 101, and waste accumulated in feet = 202 feet.

Idea -II: : A dummy heuristic for Cutting Stock Problem

We can improve it by not just fulfilling the demand order by order. Instead, we can do the following: Start with the order type of minimum length so that the leftover part from the large rod can fulfill the other item type, which leads to minimizing waste.

Its python implementation:

import numpy as np

large_size_rod_used = 0 
demand_size = [4, 6, 7]
number_of_demand_type = 3
demand_count = [80, 50, 100]
large_len = 15 
effective_len = large_len
waste = 0

def indices_of_sorted_list(s):
    return sorted(range(len(s)), key=lambda k: s[k])

# np_demand_size = np.array(demand_size)
for i in indices_of_sorted_list(demand_size):
    while (True):
        if (demand_count[i] > 0) :
            if (demand_size[i] <= effective_len):
                effective_len = effective_len - demand_size[i]
                demand_count[i] = demand_count[i] - 1
                while(True):
                    temp_remaining = [(effective_len - demand_size[j],j) for j in range(number_of_demand_type) 
                                      if  effective_len >= demand_size[j] and demand_count[j]>0]
                    if temp_remaining:
                        j = np.argmin(np.array([x[0] for x in temp_remaining]))
                        j = [x[1] for x in temp_remaining][j]
                        effective_len =  effective_len - demand_size[j]
                        demand_count[j] = demand_count[j] - 1
                    else:
                        break
                
            large_size_rod_used = large_size_rod_used + 1
            waste = waste + effective_len
            effective_len = large_len
            continue
        else:
            break
print("large_size_rod_used ", large_size_rod_used)
print("total waste ", waste)

Let us run this:
To meet the demand, the total number of large-sized rods used is = 95, and waste accumulated in feet = 105 feet. May be we are lucky and obtain the optimal solution for this particular problem. If we change the demand orders, this idea might not work. We can come up with such demand picture.

Since both methods do not use any technique that minimizes the number of large-sized rods, there is a high likelihood we will land up to the suboptimal solution.

A basic mathematical modeling approach: a foundation of Column Generation for Cuttings Stock Problem

If we define as a binary decision variable equal to 1 if th large-sized rod is used in producing small-sized rods of type , , and . If th rod does not participate in the production, we set it to 0.
Similarly, suppose and as the number of times , , and type of rods are cut from th large-sized rod.
Now, the constraints that can be obtained from the customer demand picture are

1. 
2. 
3. 
4. 
5. are binary, are positive integers.

The objective here is to minimize the sum of all the

Note that the estimated value of can be obtained from the heuristic;

If we consider . Using python CPLEX Python API, we can model and solve as follows:

import cplex
import sys

# Input data

DEBUG = True
class DATA:
    n= 100 # number of large-sized rod 
    m = 3 # number of required rod types
    small_rod_demands = [80,50,100]
    small_rod_size = [4,6,7]
    large_rod_size = [15]

class CPLEX:
    
    
    def __init__(self):
        self.model = cplex.Cplex()
        
    def solve(self):
    
        self.model.solve()
        
    def read_problem(self, problem):
    
        return cplex.Cplex(problem)
    
    def write(self, file_name):
        self.model.write(file_name)

    def get_objective_value(self):

        return self.model.solution.get_objective_value()
    
    
    def define_variable(self, varname_list, type_of_var, objective_coef_vector):
        
        n_var = len(varname_list)
        if type_of_var == "binary":
             self.model.variables.add(obj=objective_coef_vector , names =varname_list,
                        types = [self.model.variables.type.binary] * n_var )
             
        elif type_of_var == "continuous":
            self.model.variables.add(obj= objective_coef_vector, names =varname_list,
                        types = [self.model.variables.type.continuous] * n_var)
            
        elif type_of_var == "integer":
            self.model.variables.add(obj= objective_coef_vector, names =varname_list,
                        types = [self.model.variables.type.integer] * n_var)
        return None

    def define_constraint(self, the_const_names, the_rows, the_senses, my_rhs ):
        
        self.model.linear_constraints.add(lin_expr=the_rows, senses= the_senses, rhs = my_rhs, names = the_const_names)
        
        return None


class cutting_stock:
    
    def __init__(self, n, m, small_rod_demands,small_rod_size,large_rod_size):
        
        self.n = n
        self.m = m
        self.small_rod_demands = small_rod_demands
        self.small_rod_size = small_rod_size
        self.large_rod_size = large_rod_size

        self.bin_var_names = ["y_"+str(i) for i in range(n)] # binary variables
        self.int_var_name_types = [["x_"+str(i)+"_"+str(j) for j in range(n)] for i in range(m)]
        self.const_names_types = ["t_"+str(j) for j in range(m)] 
        self.const_sense_types = ["G" for j in range(m)] 
        self.const_rhs_types = small_rod_demands


        self.const_name_pattern = ["p_"+str(i) for i in range(n)]
        self.const_sense_pattern = ["L" for i in range(n)]
        self.const_rhs_pattern  = [0 for i in range(n)]
        
        self.cplexSolver = CPLEX()
    def create_mathematical_model(self):
        
        
        
        # 1. binary variable
        objective_coef_vector = [1 for i in range(self.n)]
        self.cplexSolver.define_variable(self.bin_var_names, "binary", objective_coef_vector)
    
        # 2. integer variable
        for i in range(self.m):
            objective_coef_vector = [0 for i in range(self.n)]
            self.cplexSolver.define_variable(self.int_var_name_types[i], "integer", objective_coef_vector)
    
        # add constraints
        #1. const_names_types
        for i in range(self.m):
            the_rows = [[self.int_var_name_types[i], [1 for i in range(self.n)]]]
            self.cplexSolver.define_constraint([self.const_names_types[i]], the_rows, [self.const_sense_types[i]],
                                          [self.const_rhs_types[i]])
    
        #2 const_name_pattern
        coef_list =  self.small_rod_size + [-self.large_rod_size[0]]
        for j in range(self.n):
            temp_var_name_list = []
            for i in range(self.m):
                temp_var_name_list.append(self.int_var_name_types[i][j])
    
            the_rows = [temp_var_name_list + [self.bin_var_names[j]] ,coef_list]
            self.cplexSolver.define_constraint([self.const_name_pattern[j]], [the_rows], 
                              [self.const_sense_pattern[j]], [self.const_rhs_pattern[j]])
    
    def solve_the_model(self):
        # Now time to solve it
        self.cplexSolver.solve()
        
    def write_the_model(self):
        self.cplexSolver.write("cutting_stock_integer.LP")
        
    def get_objective_value(self):
        # Get the objective function. - which is number of large-sized rod
        return self.cplexSolver.get_objective_value()
        


if __name__ == "__main__":
    if len(sys.argv) != 2:
        print("Data is not provided accuratly, solving a cutting stock problem from the default-example")
        cs = cutting_stock(DATA.n, DATA.m, DATA.small_rod_demands,DATA.small_rod_size, DATA.large_rod_size)
        # Create the model
        cs.create_mathematical_model()
        if DEBUG:
            cs.write_the_model()
        
        # Solve it
        cs.solve_the_model()
        
        # obtain the value
        print("optimal rod used", int(cs.get_objective_value()))
    else:
        extract_data_from_input_file = sys.argv[1]
        print(extract_data_from_input_file)

The solution obtained from the above script is 95 large-sized rods.

The above formulated model was already studied in 1939 by a famous mathematician “L. V. KANTOROVICH”. The paper can be downloaded from the following link: It studied for the first time “Column Generation for Cuttings Stock”

http://resistir.info/livros/kantorovich_mathematical_methods.pdf

Some important points that one can find out from the above model are:

• It is an integer linear program: Difficult problem (NP-hard problem)
• It required many constraints and variables just for the small-sized problem. In our example, for obtaining three different sizes of the small-sized rods, the number of variables generated = n + m*n = 100 + 100*3 = 400 ( for the estimate of n, which is 100).
• Approximation might not be helpful: Relaxing integer variables to Linear gives us 88 large-sized rods – A lower bound – the gap is 7. For a bigger problem, this gap will be more large.
• A practical limitation: symmetry: obtaining small-sized rods from two different large-sized rods leads to different solutions regarding variables’ values, but absolutely the same in practice. For example, in the current case, , there will be many alternate solutions to the problem with the same optimal value of 95.

Can we think of some other way to model it ?

Idea: In the previous model, more than one binaries could be combined if they belong to those large-sized rods that produces the same number/types of small-sized rods. The idea of `Pattern’ hits into our mind, right ?
Now, imagine if we have large-sized rods with various patterns instead of the number of large-sized rods. In that case. The objective is to minimize the number of such different patterns.
Objective function

Here is the number of large-sized rods with pattern
We also consider a decision variable which represents the number of small-sized rod of type in pattern .

Constraints will be:
1.

2.

3.
4. for all
In the above formulation, if the pattern information is available, the problem become an MIP and can be easily solved. Now, there are two very strong features with this model that make it widely acceptable and benefit us in solving the cutting stock problem efficiently. 1) non-symmetry, i.e., unlike the previous model, a KANTOROVICH model, we do not have different solution set set with same objective value. 2) very strong relaxation: The gap between optimum value of the model and its optimum relaxation is always less than 2 . In fact, there is no instance known with a gap greater than . This is very strong result – we do not need to solve the MIP rather just solve the LP relaxation of the model. Why?

Now let us discuss the technique, a column generation technique which solves this pattern-based formulation-

Column Generation for Cutting Stock Problem

From the previous paragraph, we got to know a mathematical formulation of the cutting stock problem which is pattern based. But the problem with this formulation is obtaining the patterns as there will be many variables/columns in the model. What, if we start with few columns and generate the new by some intelligence, if only requires (the one which gives rise the better objective value to the model)?
The algorithm, column generation or delayed column generation does this work. We solve the problem in iterations. In the initial iteration phase, we start with some intuitive valid patterns and solve the problem we call the problem master problem. To compute a better valid pattern we solve a separate problem (subproblem). We also call it a Knapsack problem. We will discuss Knapsack problem and its method to solve in other Tutorial.
To understand Column generation well, let us come back to our previous example.
We start with initial iteration:
Iteration 1:
Master:
minimize
Subject to,

To solve, we need to have a valid pattern:[80 50 100] units of [4,6,7] sized rods can be accommodated by [1 0 0], [0 ,1, 0] and [0, 0 , 1] patterns. So in that case. We redefine the model. Master becomes

Master problem:
minimize
subject to



All the variables are continuous (assume the problem is linear).

Let us solve them
But still it has many variables, let us drop the variables from the master.
We call the resulting model as a restricted master problem:

Restricted Master:
minimize
subject to



All the variables are continuous.
The optimal solution to the model is 230. the dual value to the corresponding constraints are = .
Now to check the solution is also optimal to the master problem. We need to check whether any reduced cost corresponds to the new non basic column is negative. i.e.,
. We check it for all the
For example, For column ,
reduced cost,

If we are able to find the value of , and such that the third pattern (column) is the valid one, i.e., and the respective reduced cost is negative, we can add this pattern to master.

Certainly, I can easily find at least one pattern that respects the pattern size restriction.
It is [2 0 1]. If we check the reduced cost =

Since, the reduced cost is negative, we have direction of improvement (Are you familiar with this term ? We will discuss in our Tutorial on Simplex algorithm, Later). We will add this pattern/column to the restricted master problem. When solving the updated restricted master problem, the column will replace one of the columns in the basis.

For other non-basic columns, we compute the reduced cost,

We select the column (pattern) to be added to the master problem if it leads to negative reduced costs.
Do determine it, we can write a mathematical model :

minimize
Subject to,

Where,
are integers.

If we look this sub-problem carefully, its a special problems of filling up knapsack or a bag of size (say weight) 15 unit by smaller items of different weights. The objective function coefficient associated to the associated variables are the valuation (importance) of each items. We can solve them by mathematical programming solvers or using other heuristic/dynamic programming methods, which mostly far more faster than the IP solver for large number of variables.

Let us implement column generation method and check the optimal cut of rods in our example.

A basic Column Generation for Cuttings Stock: A python Implementation for our problem

# -*- coding: utf-8 -*-

import cplex
import sys
import numpy as np

# Input data

DEBUG = True
class DATA:
    n= 100 # number of large-sized rod 
    m = 3 # number of required rod types
    small_rod_demands = [80,50,100]
    small_rod_size = [4.,6.,7.]
    large_rod_size = [15.0]
    
class CPLEX:
    
    
    def __init__(self):
        self.model = cplex.Cplex()
        self.sub_created = False
        
    def solve_model(self, master_flag):
        
        if master_flag:
            self.model.set_problem_type(self.model.problem_type.LP) # you need to specify the type of model, else it will take MIP
        else:
            self.model.set_problem_type(self.model.problem_type.MILP)
        
        self.model.solve()
        
    def write_problem(self, file_name):
        self.model.write(file_name)

    
    def get_objective_value(self):

        return self.model.solution.get_objective_value()
    
    def get_solution(self):
        
        return self.model.solution.get_values()
    
    
    def define_variable(self, varname_list, type_of_var, objective_coef_vector):
        
        n_var = len(varname_list)
        if type_of_var == "binary":
             self.model.variables.add(obj=objective_coef_vector , names =varname_list,
                        types = [self.model.variables.type.binary] * n_var )
             
        elif type_of_var == "continuous":
            self.model.variables.add(obj= objective_coef_vector, names =varname_list,
                        types = [self.model.variables.type.continuous] * n_var)
            
        elif type_of_var == "integer":
            self.model.variables.add(obj= objective_coef_vector, names =varname_list,
                        types = [self.model.variables.type.integer] * n_var)
        

    
    def define_constraint_by_row(self, the_const_names, the_rows, the_senses, my_rhs ):
        
        self.model.linear_constraints.add(lin_expr=the_rows, senses= the_senses, rhs = my_rhs, names = the_const_names)
        
        
    
    def get_dual(self):
        
        return self.model.solution.get_dual_values()
    
    def get_pattern(self,pattern_lot,n_const):
        
        return [[self.model.linear_constraints.get_coefficients(i,j) for i in range(n_const)] 
                for j in range(len(pattern_lot)) if pattern_lot[j]!=0]
        
    
    def create_sub_generate_pattern(self, coef_multiplier, n_var, large_rod_size, small_rod_size):
        
        if not self.sub_created:
            self.var_name = ["y_"+str(i) for i in range(n_var)]
            self.model.variables.add(obj=coef_multiplier,types=[self.model.variables.type.integer]*n_var,
                               names=self.var_name)
            
            row = [[self.var_name,small_rod_size]]
            the_senses = 'L'
            const_name = 'P'
            self.model.linear_constraints.add(lin_expr=row,senses=[the_senses], rhs = large_rod_size, 
                                             names= [const_name])
            
            self.model.objective.set_sense(self.model.objective.sense.maximize)
            
            self.sub_created = True
        
        self.model.objective.set_linear([(i,coef_multiplier[i]) for i in range(n_var)])
        
        self.model.solve(False) # For solving a subproblem, Pass False as argument, True is for Master 
        
        if self.get_objective_value() > 1: # Since min reduced cost = 1 - dual*variable <0:  max dual*variable - 1 >0 => max dual*variable >1
            
            return self.model.solution.get_values()
        else:
            return []
                
    def update_master(self, pattern,iteration, n_const):
        
        # add a variable to master
        self.model.variables.add(obj=[1],types=[self.model.variables.type.continuous],
                               names=['y_'+str(iteration)], columns=[[[i for i in range(n_const)],pattern]])
        


class cutting_stock_column_generation:
    
    def __init__(self, n, m, small_rod_demands,small_rod_size,large_rod_size):
        
        self.n = n
        self.m = m
        self.small_rod_demands = small_rod_demands
        self.small_rod_size = small_rod_size
        self.large_rod_size = large_rod_size
        
        self.master_flag = True
        self.initial_pattern = np.identity(m) # different demand types are m
        
        # initialize restricted master 
        self.int_var_pattern_count = ["y_"+str(i) for i in range(m)] 
        self.const_names_types = ["t_"+str(j) for j in range(m)] 
        self.const_sense_types = ["G" for j in range(m)] 
        self.const_rhs_types = small_rod_demands

        self.cplexSolver1 = CPLEX() # For master
        self.cplexSolver2 = CPLEX() # For sub
    
    def create_restricted_master_model(self):    
        
        # 1. number of types of patterns
        objective_coef_vector = [1 for i in range(self.m)]
        self.cplexSolver1.define_variable(self.int_var_pattern_count, "continuous", objective_coef_vector)
    
        
        # add constraints
        #1. const_names_types
        for i in range(self.m):
            the_rows = [[self.int_var_pattern_count, list(self.initial_pattern[i])]]
            self.cplexSolver1.define_constraint_by_row([self.const_names_types[i]], 
                                                             the_rows, [self.const_sense_types[i]],
                                          [self.const_rhs_types[i]])
        
    def iterative_loop(self, WRITE_DEBUG):
        
        # get the dual values of the initial restricted master:
        # solve the initial master
        objvalue =0.
        dual_value = self.cplexSolver1.get_dual()
        pattern = self.cplexSolver2.create_sub_generate_pattern(dual_value, self.m, self.large_rod_size, 
                                                               self.small_rod_size )
        
        if WRITE_DEBUG:
            self.cplexSolver1.write_problem("initial_master.LP")
            self.cplexSolver2.write_problem("initial_sub.LP")
        column =  self.m
        while(pattern):
            if pattern:
                
                self.cplexSolver1.update_master(pattern,column, self.m)
                self.cplexSolver1.solve_model(self.master_flag)
                dual_value = self.cplexSolver1.get_dual()
                pattern = self.cplexSolver2.create_sub_generate_pattern(dual_value,self.m, self.large_rod_size, 
                                                                       self.small_rod_size )
                column = column + 1
                if WRITE_DEBUG:
                    self.cplexSolver1.write_problem("initial_master_"+str(column - self.m)+".LP")
                    self.cplexSolver2.write_problem("initial_sub_"+str(column - self.m)+".LP")
                
            else:
                objvalue =  self.cplexSolver1.get_objective_value()
                break
        return objvalue, pattern
    
    def solve_the_model_master(self):
        # Now time to solve it
        self.cplexSolver1.solve_model(self.master_flag)
        
    def get_solution(self):
        return self.cplexSolver1.get_solution()
        
    def get_objective_value(self):
        # Get the objective function. - which is number of large-sized rod
        return self.cplexSolver1.get_objective_value()
        
    def get_pattern(self,pattern_lot):
        
        # Get columns
        return self.cplexSolver1.get_pattern(pattern_lot, self.m)

if __name__ == "__main__":
    WRITE_DEBUG = True
    if len(sys.argv) != 2:
        print("Data is not provided accuratly, solving a cutting stock problem from the default-example")
        cs = cutting_stock_column_generation(DATA.n, DATA.m, DATA.small_rod_demands,DATA.small_rod_size, DATA.large_rod_size)
        # Create the model
        cs.create_restricted_master_model()
        #if DEBUG:
         #   cs.write_the_model_master("initial_restricted_master.LP")
        
        cs.solve_the_model_master()
        cs.iterative_loop(WRITE_DEBUG)
        
        # obtain the value
        print("optimal rod used", int(cs.get_objective_value()))
        
        pattern_lot = cs.get_solution()
        print("optimal pattern lot", cs.get_solution())
        
        print("optimal pattern", cs.get_pattern(pattern_lot))
    else:
        extract_data_from_input_file = sys.argv[1]
        print(extract_data_from_input_file)

The optimal solution we get is 95 rods and the patterns are: [[2.0, 0.0, 1.0], [0.0, 2.0, 0.0], [0.0, 0.0, 2.0]]

Fork the above code from my git repository for your use.

Other benefit in using Column generation technique and its application apart from Cutting stock problem

• Obtain lower and upper bounds of the pattern of large-sized rod used and so its partial solution without completely solving the problem
• Adapting heuristic in the solving process – knapsack problem can use any dynamic/heuristic method for speeding up the solving time
• For most of the mathematical models where number of columns are very large, column-generation can be the preferred option to try.

If you like this tutorial, connect me at [email protected], [email protected]. We will love your input.

Click here for Some other interesting mathematical topics